FOOTBALLNOMICS: An Economic Approach to Roster Management, Part 2
The Steady State, or "How to Know When You're in a Competitive Window or a Rebuilding Cycle"
Last week, I introduced a framework for college football roster management using an Overlapping Generations Model. Specifically, I focused on the problem of how to develop players now while maintaining a high level of competitiveness on the field, and the associated trade-offs in that decision. After some shortcuts through the algebra, we arrived at the fundamental equation, which provides an mathematical link between the optimal level of player development and a team’s ability to produce more wins with additional higher-quality snaps.
The quality of snaps a team can put on the field next season is a function of how much they develop their prospects. The optimal level of development (relative to playing time) for prospects depends on how well the team converted player snaps to wins this season, how many more wins they would contribute with higher-quality snaps, and their strategy and coaching.
This result, well-grounded in theory (read: also easily derived from common sense), is interesting and useful because it provides us with a systematic approach to understanding how choices in player utilization relate to wins across multiple seasons. Coaches, as we know, have to plan and build not just for this season, but for next season and the next.
While last week’s result was a nice start, there are obvious complexities for application. I’ll start to add some wrinkles here to increase our model’s sophistication and help us along the path to better understanding the problem of building a roster in the modern college football landscape.
NOTE: If you haven’t read last week’s installment, I’m going to build on it. Go here, give it a quick read, then come back.
Models are Like Onions
To paraphrase the great poet, models are like onions. Last week, we talked about what a model, in the economic sense, is: a structured system defined mathematically to help identify important facts and features of the world. It’s a simplification of reality that helps us isolate interesting dynamics. Those models, as you get closer and closer to reality, become increasingly complex. There are layers. Like onions.
The economist’s problem is less “how do I make a perfect representation of reality?”, and more “how do I create the most tractable model that provides insight into general truths about reality?” Adding complexity is not an exercise in improving predictive quality, but rather a decision-process about which facets of reality are most important to explicitly model, while keeping the model solvable. Once you’ve well-grounded your theoretical model, then you can get to the data and employ approaches from statistics and data science to work on prediction and enhance your model.
This week’s onion layer in the model will be two-fold. First, I’ll put some functional forms on the abstract notions of utility u(.) and production f(.). Then, with those closed forms, we’ll be able to look at the Steady State, the optimal level of player development and playing time that maximizes your discounted sum of wins across the foreseeable horizon.
These additions, while increasing the complexity of the model, will allow us to represent the developmental nature of college football: Yes, every coach wants to put the as many of the best players on the field as he can (football is easy!), but in reality, there are constraints about which players you can get, physical laws governing player development and readiness, and football reasons to strategically employ players differently across different timelines.
Log Utility - More is better, but not always by a lot.
Log utility is a useful representation of preferences. For a player, playing 15 snaps a game instead of 0 snaps a game brings a lot of benefit! But, for that same player, the difference between 65 and 67 snaps a game is small, up to the point where there might be such a small difference in benefit between two large numbers it’s negligible. This form is used often in economics thanks to its usefulness in displaying the concept of diminishing returns. More is better, but a lot more is not always better. Imagine you’re at a football game in Texas in August, say an 11 am kickoff. You’re hot, baked by the sun. That first cold bottle of water from the concession stand is well worth your $6. That second cold bottle of water might take you to peak enjoyment, cooling and refreshing. But that third bottle of water? Well, now you’ve spent $18 total and you’ve got a lot of water sloshing in your stomach. The fourth? Ok, man, what are we doing with all this water? That’s the concept of diminishing returns. Same good, different utility relative to amount.
When we convert the player level utility function to the log, we get an optimal level of player development that’s not dependent on vague functions, but on specific parameters. Again, skipping some boring algebra, we this result in equilibrium.
The optimal level of player development this period (time t) is a function of that player’s opportunity provided by the program (in terms of development and converting snaps to wins) and of the discount factor - how much a program values wins now against wins later.
Given that the discount factor B is between 0 and 1, B/(1+B) will be less than 1, which means it will always be optimal to develop younger players to some extent. This feels obvious, but again, mathematical representations of the obvious are useful!
A larger discount factor, meaning we value future wins similarly to present wins, means that we will, in the equilibrium, want to develop younger players more. This aligns nicely with the aforementioned problem of competitive windows. If we know this season is a rebuilding year [don’t worry, we’ll talk about how to identify that in a minute], then we value future wins more, and we want to develop our players more.
The Other Side of the Coin: Cobb-Douglas Production
We need to talk about that w_t above, what I’ve referred to as “a player’s opportunity provided by the program”. In these growth models, this is the wage, the “cost” of labor. It makes sense, firms pay households, households use that wage to either save or consume. But because here I’m playing fast and loose with some traditions of economic growth modelling, we’ve conceived the problem from a more centralized place, where player decisions are made by the team. I’ll get to an economic approach to player compensation soon enough, but in this model, that “wage” paid to players is related to their playing time on the field and development, not their financial compensation. So we have to get abstract here for a little bit.
In this model, we conceive of that wage as what the team can offer a player in terms of playing time and development. It’s a good motivating factor for a lot of recruits, choosing schools based on how many NFL draft picks they’ve put out at that position, for example.
How do we represent that w_t, which is so informative above for the optimal level of player development? Cobb Douglas utility helps us there. College football teams convert players (labor) and productive snaps (capital) into wins like this:
Where k_t is the productive snaps of each player, A is the program specific technology - that is, strategy, facilities, strength and conditioning, analytics, etc - and alpha is the marginal productivity of quality snaps: how much more wins you get by adding more quality snaps. Alpha will be between zero and one, and so you can see that we also have diminishing returns here. That makes sense. If you’re Kent State and you add a five star senior defensive end, there are huge wins gains to be made! If you are Ohio State and you add a five star senior defensive end, you’ll be better, but not by anywhere near the magnitude of Kent State’s improvement.
Solving the team’s optimization problem1, in equilibrium the opportunity provided to a player is a function of that marginal productivity, team technology, and the level of quality snaps we’re putting on the field today.
Plugging this back into the player development equation, we find that the optimal level of player development in turn depends on these factors!
Ok, so what?
Now that we have closed forms for the optimal level of player development with log utility (diminishing returns), we can revisit our central equation, the equation that tells us how the quality of productive snaps in future seasons relates to the quality of future snaps this season.
In layman’s terms, the quality of our team next season depends on:
How much we value wins today relative to wins in the future (Beta)
The marginal productivity of additional quality snaps (alpha)
Our team technology (strategy, facilities, strength and conditioning, analytics, etc)
The level of quality snaps we put on the field this season
Which is a neat result! We have a path. Thinking in this framework, we’re not just looking at every season as a random group of unaffiliated players, but instead as a path-dependent sequence where our choices today affect our quality in the future. That’s crucial for effective roster management. You have to be able to think about the entire horizon, not just live year to year, scrambling for answers.
The Steady State, or “How to Know When You're in a Competitive Window or a Rebuilding Cycle”
There are some fun dynamics from the above equation we could play with. What happens if we improve our team technology by hiring an analytics director? What changes if we want to be more competitive in the short-term (decrease our discount factor)? What lessons about talent acquisition could we learn by incorporating team-specific marginal productivity?
Those are all on the table, but for now, I want to focus in on the cycles.
Aside from Nick Saban’s Alabama2, college football success is a multi-year process of development, close losses, and building foundations for the future. Any team’s peak run - Washington, TCU, Cincinnati, LSU in 2019, Michigan State’s playoff appearance that feels eons ago - is going to coincide with the bulk of your talent being experienced and developed at the same time.
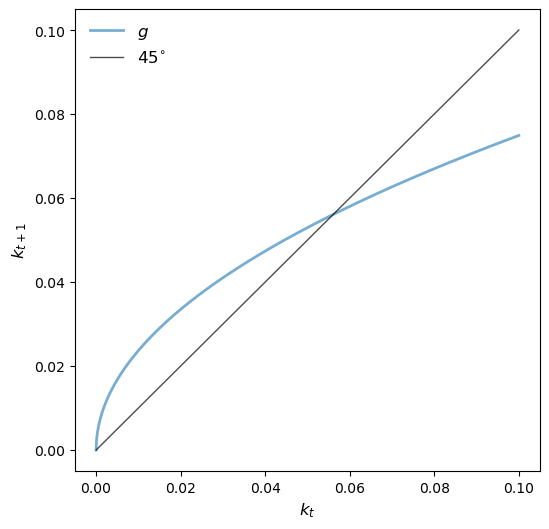
The equation that governs how your team is going to peak and rebuild comes from the idea of the steady state. The steady state just refers to the level where your productive snaps next season (k_t+1 above) is the same as your productive snaps this season (k_t).
If on the graph above, you imagine the BLUE LINE is our central equation and the BLACK LINE is where productive snaps today and productive snaps tomorrow equal each other, there is a natural STEADY STATE (k*) where the two cross. Now, the steady state in general, the idea of this year’s productive snaps equaling next year’s productive snaps, is not exactly something to aspire to - for example, if you’re bad this year, you certainly don’t want to put the same product on the field again, if you can help it.
What the steady state is, instead, is the representation of the optimal flow of productive snaps. When you’re good, you want to be maintaining competition and developing across multiple years.
If a team’s productive snaps this year is below the steady state (k_t < k*), meaning you don’t have as many productive snaps as you’d like, then you want to increase development to increase k_t+1, which will in turn, push up k_t+2… and so on, until you reach that steady state where you’re optimizing your development process and consistently competitive across periods.
On the other hand, if your productive snaps this season is above the steady state (k_t > k*), you can afford to play prospects more and focus less on development, as you try to optimize for the current competitive window.
Pulling it All Together
Again, if you’ve read this far and you’re still following, congrats - my class features a participation grade and you’re getting an A. If you’re not, no worries, I’ll do my best here to summarize what we’ve done and where we can go from here, and you can always make it up with a good grade on the final.
In today’s installment, we introduced two onion layers to the overlapping generations model:
First, we formalized the idea of diminishing returns to playing time (for players) and productive snaps (for teams). This is a key step in a model that extends to reality, because, in the words of Bill Belichick: “We are not collecting talent; we’re building a team.” It’s not enough to just grab stars and hope for the best, we want to have a foundation to understand HOW those players fit in our system and HOW that will translate to wins now and in the future.
Second, we introduced the idea of the steady state and found an equation to help us understand development cycles. Teams want to compete every year, but the nature of talent and variance in college football means there are trade-offs. Using the idea of the steady state and our central equation - which links quality snaps on the field across seasons - helps us understand how the development cycle is progressing and how we should adjust our decisions about player development and playing time to optimize.
Overall, what we have after two installments is a functioning model that can be used to understand how teams make decisions across seasons in player development and can help quantify the exact process of development cycles and competitive windows in college football.
One glaring limitation - among many - so far is of course the simple truth that not all players are created equal. Next week, we’ll introduce some positional differences in prospects and starters, demonstrating how we can account for the rates at which different players contribute and develop to teams.
At some point, I’ll stop apologizing just for skipping the algebra. Trust me, it’s less laziness and more that I think it will just actively drive people away from reading.
A common theme in my work: Highlighting how the sheer inexhaustible dominance of Saban’s teams broke a lot of people’s brains with how we think about success.